时空和物质怎么调和共舞华尔兹？《张朝阳的物理课》推导爱因斯坦场方程

  原标题：时空和物质怎么调和共舞华尔兹？《张朝阳的物理课》推导爱因斯坦场方程

  怎么用张量描绘时空曲折？什么是黎曼曲率张量？物质的能动张量又怎么将之联络而构成爱因斯坦场方程？12月29日12时，《张朝阳的物理课》第193期开播，搜狐创始人、董事局主席兼首席执行官、物理学博士张朝阳坐镇直播间，首要回忆了广义相对论的结构，介绍了爱因斯坦场方程的结构。一起，经过与牛顿第一定律相比较，再次强调了测地线的重要性。然后，张朝阳具体地推导并讲解了黎曼曲率张量的意义。紧接着，在介绍了黎曼曲率张量的缩并后，张朝阳依据能动张量的守恒性质和比安基恒等式（Bianchi identities），给出了爱因斯坦张量，并假定爱因斯坦张量正比于能动张量。最终，在弱场近似的条件下，张朝阳比较了测地线方程和牛顿引力下的泊松方程，获得了爱因斯坦张量与能动张量的份额系数，至此完好地推导出了爱因斯坦场方程。

  爱因斯坦提出广义相对论已有百年，各种试验都证明晰其正确性。最早，爱丁顿观测日全食验证了光线偏折、爱因斯坦解说了水星近日点的反常进动。在近现代，世界微波布景辐射阐明晰广义相对论下世界学的合理性，而现在LIGO至今观测到了上百个引力波事情、多个脉冲双星高精度地验证了广义相对论的四极矩辐射、脉冲星计时阵列（Pulsar Timing Array，简称PTA）查找到了随机引力波布景、人类拍照了超大质量黑洞人马座A星和室女座A星的相片、将近50年的高精度地月激光测距、S2绕人马座A星的进动、信使号（MErcury Surface, Space ENvironment, GEochemistry, and Ranging，简称MESSENGER）水星探测器高精度观测水星近日点的进动等试验都验证了广义相对论的正确性。饱尝住了如此多试验的检测，足以证明广义相对论在描绘引力的结构中具有适当的卓越性。

  在广义相对论中，引力不再是一种力，而是时空的曲折，这种时空曲折的程度由爱因斯坦场方程描绘

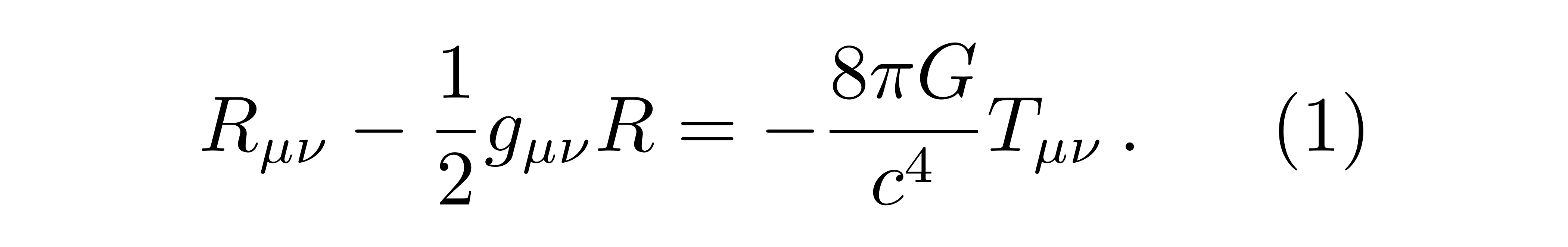
  其间方程左面第一项是里奇曲率张量，g是度规，方程右边T是物质的能动量张量。（请注意，方程右边的负号源自于里奇张量是黎曼曲率张量的第2个目标r和第3个目标t缩并后带来的。若里奇张量界说为黎曼曲率张量的第1个目标s和第3个目标t缩并，则方程右边不可能会呈现负号。黎曼曲率张量请看公式（15）。）粒子若在时空中不受外力运动，则其由测地线方程描绘

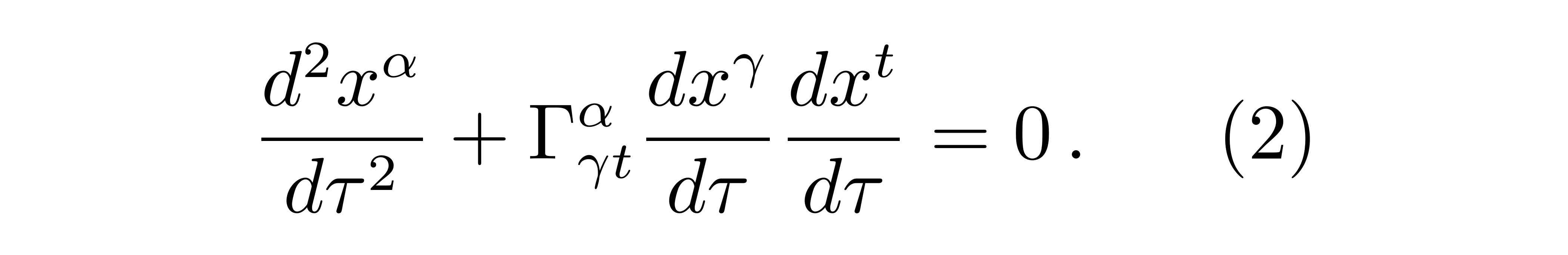
  求解出爱因斯坦场方程（1），即得到度规g的方法，咱们将其代入到上述方程（2）中的克氏符中并求解出粒子的坐标，即可计算出粒子的运动轨道，而进一步便可获取其速度。

  咱们先了解方程（1）左面黎曼曲率张量的几许意义。一个协变矢量V在一个空间中沿着一条方向为r的曲线从P平移到R点，假定这一段很小，则适当于坐标做了如下改变

  这儿的第一项是一个一般导数，第二项可了解为因为基矢改变而导致的矢量V的改变。此二阶张量DV的重量可表明为一个4x4的矩阵。假如矢量V再沿着方向为s的曲线从R点平移到S点，依旧假定这一段途径很小，则适当于坐标又做了如下改变

  现在咱们类似地让矢量V平移两次，但先沿着方向为s的曲线点，再沿着方向为r的曲线平移dx抵达S点，则新的矢量V 为

  （请注意，先沿着方向为s的曲线平移dx，再沿着方向为r的曲线平移dx，与先沿着方向为 r的曲线平移dx，再沿着方向为s的曲线平移dx，这四条边在无挠率（torsion free）的情况下可构成一个关闭的平行四边形，在有挠率的情况下则不可。）接着咱们把这两个矢量V公式（7）和V公式（9）相减得到

  这两种平行移动的起点和结尾相同，仅仅途径不同，在曲折时空中，沿着不同的途径平移就会导致矢量的误差。为了愈加形象地阐明这个现象，张朝阳先在一张平直的白纸上画了一系列平行的向量，再剪去一个缺口，将白纸粘合构成一个圆锥。他发现，原先平行的矢量在缺口处不再平行，矢量绕着这个圆锥走一圈后，与原矢量不相同了。或者说，从纸上某点P顺时针绕过锥顶来到坐落缺口的点S，和逆时针绕过锥顶来到点S，得到的矢量是有不同。

  方程（12）阐明，一个矢量的二阶协变导数交流次第后发生的三阶张量，等于一个四阶的张量与矢量本身的缩并。依据方程（12），可将协变导数表明为一般导数和克氏符的组合

  因为矢量V 是恣意的，因而黎曼曲率张量能够表明为克氏符沿两个方向的导数之差加上克氏符的乘积之差

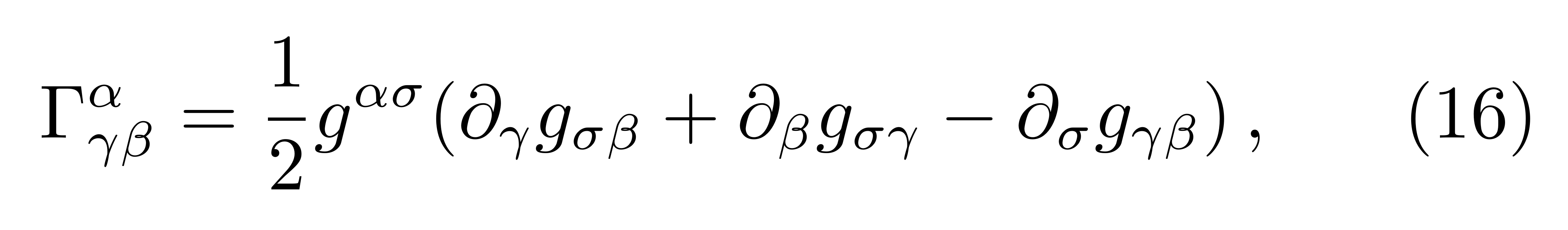
  可看出克氏符是度规的一阶导数，而黎曼曲率张量（15）则是度规的二阶导数。咱们再回忆一下度规的界说，它是标架的缩并

  黎曼曲率张量是一个四阶的张量，而能动张量是一个二阶的张量，它们之间欠好直接联络。为了让这两个张量发生直接的联络，最简略的方法是将黎曼曲率张量（15）从4阶缩并（contraction），即让目标t与r相同，降到2阶张量，以及对此二阶张量费用规所并得到零阶标量，

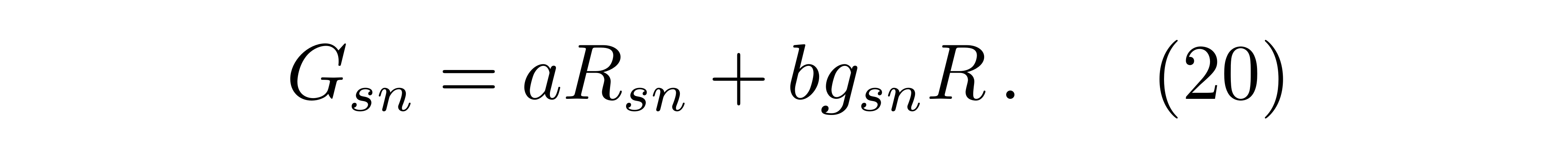
  G是一个二阶对称张量，带下目标s和n的R也是一个对称张量，称之为里奇张量（Ricci tensor），最终一个标量R称之为里奇标量。

  上节课张朝阳现已介绍了能动张量各个重量的物理意义，即能动张量T的00重量表明物质的单位体积内的包括的能量，0i重量表明沿空间i方向上的能流密度，ij重量代表动量密度的i重量在j方向上的改变率，这些部分需满意能量动量守恒定律，即能动张量的散度为零

  此刻将公式（20）界说的张量G中的份额系数a除到后边的两个系数中，由此咱们得到了更简练的方法

  在黎曼几许中存在两个关于黎曼曲率张量的恒等式，即比安基恒等式和里奇恒等式：

  为确认待定系数c2，咱们咱们能够考虑弱场极限，此刻广义相对论应回到牛顿引力，引力势能满意泊松方程

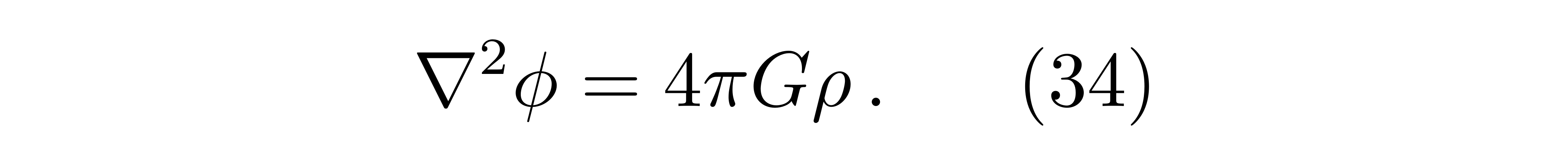
  泊松方程中呈现了物质的密度，而在能动量张量中，00重量代表物质的密度，这提示咱们爱因斯坦场方程的00重量应该能在弱引力下退化为牛顿引力中的泊松方程。

  公式（35）中微扰项的h除00重量非零外，别的的重量都为0，代入到里奇张量中得到

  其间左面方程的最终一步用到了泊松方程（34）。比照两头的方法可得待定系数c2为

  据了解，《张朝阳的物理课》于每周周五、周日正午12时在直播，网友能够在APP“重视流”中查找“张朝阳”，观看直播及往期完好视频回放；重视“张朝阳的物理课”账号，检查课程中的“知识点”短视频；此外，还能够在搜狐新闻APP的“搜狐科技”账号上，阅读每期物理课程的具体文章。回来搜狐，检查愈加多